Канонический анализ

Поиск в справочнике по интернет-статистике

Введение в канонический анализ

Существует много показателей корреляции, выражающих связь между двумя или более переменными. Например, стандартный коэффициент корреляции Пирсона ( r ) измеряет скорость линейных отношений между двумя переменными. Существует множество непараметрических мер зависимости, основанных на сходстве двух переменных. глава Множественная регрессия позволяет изучать связь между переменной зависимости и набором независимых переменных. в то время как многомерный анализ соответствия это помогает объяснить взаимодействия, происходящие в наборе качественных переменных.

Каноническая корреляция является дополнительной процедурой для оценки взаимосвязи между переменными. В частности, этот анализ позволяет изучить взаимосвязь между двумя наборами переменных. Например, в педагогическом исследовании исследователь может захотеть оценить (одновременно) взаимосвязь между тремя показателями способности к обучению и пятью показателями успеха в обучении. Социологу может быть интересна связь между двумя предикторами социальной мобильности, полученными в ходе интервью, и фактической незначительной социальной мобильностью, измеренной четырьмя другими показателями. В медицинских науках можно изучить взаимосвязь между различными факторами риска и появлением определенной группы симптомов. Во всех этих случаях исследователь интересуется взаимосвязью между двумя наборами переменных, к которой анализ соответствующих методов анализа является канонической корреляцией.

В следующих темах мы кратко представим основные понятия и статистику при анализе канонической корреляции. Предполагается, что читатель знает коэффициент корреляции, который описан в модуле Основные статистические данные и таблицы и общие последствия множественной регрессии, которые описаны в модуле Множественная регрессия ,

Методы расчета и результаты

Теперь мы обсудим некоторые вычислительные вопросы, связанные с канонической корреляцией и основными результатами, которые обычно даются.

Собственные ценности. При извлечении канонических корней рассчитываются собственные значения . Их можно интерпретировать как пропорцию дисперсии, объясняемой корреляцией между соответствующими каноническими переменными. Отметим, что пропорция t рассчитывается по отношению к дисперсии канонических переменных, то есть взвешенных значений сумм двух наборов переменных; Собственные значения не говорят нам, насколько велико изменение в множестве переменных. Мы рассчитываем столько же наших собственных значений, сколько существует канонических корней, то есть столько же, сколько минимальное количество переменных в каком из двух множеств.

Следующие собственные значения будут все меньше и меньше. Сначала мы рассчитываем веса, которые максимизируют корреляцию двух значений суммы. После того, как первый элемент идентифицирован, мы находим веса, которые дают вторую наибольшую корреляцию между значениями суммы, с оговоркой, что следующий набор итоговых значений не коррелирует с предыдущим, и так далее.

Канонические корреляции. Мы интерпретируем квадратные корни наших собственных значений как коэффициенты корреляции. Поскольку эти корреляции относятся к каноническим переменным, они называются каноническими корреляциями . Как и внутренние значения, корреляции между последовательно разветвленными каноническими переменными становятся меньше. Следовательно, в качестве общего показателя канонической корреляции между двумя наборами переменных предполагается наибольшая корреляция, то есть для первого элемента. Тем не менее, другие канонические переменные также могут быть коррелированы осмысленно и интерпретируемо (см. Ниже).

Основные элементы Проверка актуальности канонических корреляций основана на простом принципе. Индивидуальные канонические корреляции проверяются индивидуально, начиная с самой большой. Только те элементы, которые являются статистически значимыми, оставлены для интерпретации. На самом деле характер теста на материальность немного отличается. Сначала оценивается значимость всех элементов, затем элементы, оставшиеся после удаления первого элемента, второго элемента и т. Д.

Некоторые авторы подвергли критике эту последовательную процедуру проверки релевантности канонических элементов (например, Harris, 1976). Однако эта процедура была «реабилитирована» в последующем исследовании Монте-Карло, проведенном Мендосом, Маркосом и Гонтером (1978).

Короче говоря, результаты этого исследования показали, что эта процедура тестирования выявляет сильные канонические корреляции в большинстве случаев, даже при относительно небольших тестах (например, n = 50). Для выявления как минимум 50% случаев худших канонических корреляций (например, R = .3) требуются более крупные выборки ( n > 200). Мы отмечаем, что небольшая каноническая корреляция имеет практическое значение, поскольку фактические различия в данных очень незначительны. Ниже мы обсудим проблему и проблему размера выборки.

Канонические весы. После определения количества важных канонических корней возникает вопрос, как интерпретировать каждый (существенный) корневой элемент. Давайте вспомним, что каждый корень на самом деле представляет две взвешенные суммы, по одной для каждого набора переменных. Один из способов интерпретации значения канонического принципа состоит в том, чтобы взглянуть на веса для каждого набора. Эти веса называются каноническими весами .

Как правило, чем больше вес (то есть абсолютное значение шкалы), тем больше положительный или отрицательный вклад переменной в сумму. Чтобы упростить сравнение весовых коэффициентов, канонические весовые коэффициенты обычно приводятся для стандартизированных переменных, то есть для переменных со средним значением 0 и стандартным отклонением 1 .

Если читатель знает множественная регрессия он может интерпретировать канонические веса таким образом, что бета-веса интерпретируются в уравнении множественной регрессии. В некотором смысле они представляют элементарные корреляции переменных с данным каноническим корнем. Если читатель знает факторный анализ он может интерпретировать канонические веса таким образом, что значения факторных факторов интерпретируются. Суммируя, канонические веса позволяют понять структуру каждого канонического корня, то есть позволяют понять, каков конкретный вклад каждой переменной в каждом наборе в данную взвешенную сумму (каноническая переменная).

Канонические ценности. Канонические веса также могут быть использованы для расчета фактических значений канонических переменных; то есть мы можем просто использовать эти веса для вычисления соответствующих сумм. И давайте вспомним, что канонические веса обычно задаются для стандартизированных переменных (преобразованных с помощью преобразования z ).

Факторная структура. Другой способ интерпретации канонических корней состоит в том, чтобы увидеть простые корреляции между каноническими переменными (или факторами ) и переменными в каждом наборе. Эти корреляции также называются факторными зарядами . Рассуждения здесь основаны на том факте, что переменные, которые сильно коррелируют с канонической переменной, имеют более общие значения. Поэтому мы должны уделять им больше внимания, когда интерпретация данной канонической переменной является значительной. Этот метод интерпретации канонических переменных идентичен тому, который используется для интерпретации факторов в факторный анализ.

Факториальная структура и канонические веса. Иногда канонические веса для переменной s близки к нулю, и соответствующий заряд для этой переменной очень велик. Может появиться и противоположная система результатов. С самого начала такой результат может показаться противоречивым; давайте вспомним, однако, что канонические веса соответствуют конкретному вводу каждой переменной, в то время как заряды канонического фактора представляют простые общие корреляции. Например, предположим, что в целях удовлетворения мы поменяли два вопроса, которые фактически говорят об одном и том же: 1) Довольны ли вы своим начальством? и (2) ты доволен своими боссами? Конечно, оба показателя очень избыточны. Когда программа вычисляет весовые коэффициенты для итогов (канонических переменных) в каждом наборе, чтобы они были максимально коррелированы, ей «нужен» только один из этих индексов, чтобы ввести диапазон, который они измеряют. Когда первой шкале присвоен большой вес, ввод второго индикатора является избыточным; следовательно он получит ноль или очень канонические веса. Тем не менее, если мы посмотрим на простые корреляции между соответствующими значениями суммы и двумя показателями (то есть факторных нагрузок ), они могут быть значительными в обоих случаях. Допустим, канонические веса соответствуют конкретным входам соответствующих переменных для данной взвешенной суммы или канонической переменной; заряды канонического фактора соответствуют общей корреляции соответствующих переменных с канонической переменной.

Дисперсионная дисперсия. Как мы уже писали ранее, коэффициент канонической корреляции относится к корреляции между взвешенными суммами двух наборов переменных. Ничто не говорит нам, сколько вариаций (дисперсий) этих переменных объяснений имеет каждый канонический корень. Мы можем, однако, вывести долю дисперсии, которая отделена данным элементом от каждого набора переменных, анализируя заряды канонического фактора. Давайте вспомним, что эти значения представляют корреляции между каноническими переменными и переменными в соответствующем наборе переменных. Если мы возведем эти корреляции в квадрат, числа, которые мы получим, отражают пропорцию вариаций каждой вариации. Для каждого элемента мы можем извлечь среднее из этих пропорций по переменным, чтобы мы получили представление о том, сколько вариаций усредняет каноническая переменная в этом наборе переменных. Другими словами, мы можем рассчитать таким образом среднюю долю дисперсии, различимой каждым элементом.

Избыточность. Канонические корреляции могут быть возведены в квадрат для расчета доли дисперсии, объясняемой общими значениями (каноническими переменными) в каждом наборе. Если мы умножим эту пропорцию на долю выделенной дисперсии, мы получим меры избыточности , то есть насколько избыточен один набор переменных для данного другого набора переменных. В форме уравнения вы можете выразить избыточность как:

Избыточность = [ 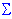(Adunkilewy2) / р] * Rc2
Ремонт с резервированием = [ 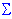(Adunkiprawy2) / д] * Rc2

В них p - количество переменных в первом (левом) наборе переменных, а q - количество переменных во втором ( правом ) наборе переменных; Rc2 - квадрат соответствующей канонической корреляции.

Обратите внимание, что мы можем вычислить избыточность первого ( левого ) набора переменных во втором ( правом ) наборе и избыточность второго ( правого ) набора переменных в данном первом ( левом ) наборе. Поскольку последовательно изолированные канонические корни не коррелированы, мы можем суммировать избыточность после всех (или только первых существенных) элементов, чтобы получить простой индекс избыточности (как предложено Стюартом и Лавом, 1968).

Значительно практично. Мера избыточности также полезна для оценки практической значимости канонических элементов. Для больших тестов (см. Ниже) канонические корреляции порядка R = .30 могут быть статистически значимыми (см. Выше). Если мы возведем этот коэффициент в квадрат ( R-квадрат = .09 ) и введем его в уравнение избыточности, показанное выше, будет ясно, что такие канонические корни объясняют лишь небольшую часть вариации. Конечно, окончательная оценка того, что представляет собой, а что нет, имеет практическое значение, носит субъективный характер. Однако, чтобы реально оценить, сколько отклонений (следующих переменных) канонический корень может объяснить, следует помнить о степени избыточности, то есть о том, насколько фактическая изменчивость в одном наборе переменных объясняется другим.

Предположения

Следующие соображения являются кратким изложением только наиболее важных предположений о канонической корреляции и основных угроз надежности и достоверности результатов.

Rozkady. Критерии значимости канонических корреляций основаны на предположении, что распределение переменных в популяции (из которой была взята выборка) является многомерным нормальным. Мало что известно о последствиях нарушения идеи многомерной нормальности. Однако при достаточно больших тестах (см. Ниже) результаты канонического корреляционного анализа обычно устойчивы.

Размеры зонда Стивенс (1986) очень тщательно рассмотрит размеры выборки, которые необходимо использовать для получения надежных результатов. Как упоминалось ранее, если в данных имеются сильные канонические корреляции (например, R> 0,7 ), даже в случае небольших испытаний (например, I> n = 50), они в большинстве случаев будут обнаружены. Однако, чтобы получить достоверные оценки канонического фактора (интерпретации), Стивенс рекомендует как минимум в 20 раз больше случаев, чем переменных в анализе, если мы хотим интерпретировать только самые важные канонические корни. Чтобы получить надежные оценки для двух канонических корней, Barcikowski и Stevens (1975) рекомендуют, основываясь на методе Монте-Карло, анализировать в 40–60 раз больше случаев, чем переменных.

Случаи выделяются. Внешние случаи могут влиять на размер коэффициентов корреляции. Поскольку анализ канонической корреляции основан на коэффициентах корреляции, они также могут серьезно влиять на канонические корреляции. Конечно, чем больше количество попыток, тем меньше влияние одного или двух случайных случаев. Тем не менее, стоит изменить различные диаграммы рассеяния, чтобы обнаружить потенциальные выбросы (как показано на анимации ниже).

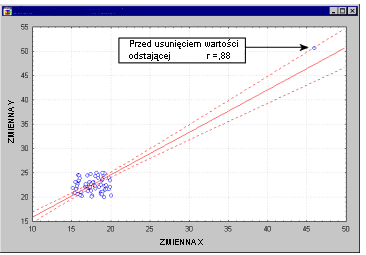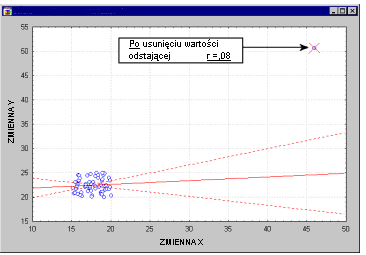
Смотрите также эллипс зоны доверия ,

Кондиционирование матрицы. Одна из причин состоит в том, что переменные в двух наборах не должны быть избыточными, то есть они должны быть в значительной степени независимы друг от друга. Например, если мы введем в какой набор одну и ту же переменную дважды, неясно, как им назначен каждый из различных весов. В смысле вычислений такие избыточные сбои анализа канонической корреляции. Если в матрице корреляции имеются совершенные корреляции или если одна из многих корреляций между одной переменной и другой является идеальной ( R = 1,0 ), то матрица корреляции не может быть обращена и канонический анализ не может быть выполнен. Такие корреляционные матрицы называются условными .

Предположение о независимости часто близко к нарушению (то есть коэффициент множественной корреляции одной из переменных с другой является «близким» 1), когда анализ включает в себя очень сильно избыточные измерения, что часто имеет место при анализе ответов на вопросник.

Общие идеи

Мы представляем, что проводим исследование, в котором мы измеряем удовлетворенность работой с помощью трех вопросников, а удовлетворенность в различных других областях жизни - с помощью семи других вопросов. Общий вопрос, на который мы хотим ответить, состоит в том, какова связь между удовлетворенностью работой и удовлетворенностью в других областях.

Всего значений

Первый подход, который мы могли бы применить, состоит в том, чтобы добавить ответы на вопросы об удовлетворенности работой и соотнести эту сумму с ответами на все другие вопросы об удовлетворенности. Если бы корреляция между двумя суммами была статистически значимой, мы бы сказали, что удовлетворенность работой связана с удовлетворенностью в других областях.

На самом деле это скорее "грубый" вывод. Мы до сих пор ничего не знаем об отдельных областях удовлетворенности, которые связаны с удовлетворенностью работой. Фактически, просто добавляя индикаторы, мы можем потерять важную информацию. Например, мы можем представить, что у нас есть два вопроса: один удовлетворен отношениями с супругом, а другой удовлетворен финансовым положением. Добавление их друг к другу напоминает, конечно, добавление «яблок к апельсину». Это означает, что человек, который недоволен финансовым положением, но доволен своей зрелостью, может состоять из людей, которые довольны финансовым положением, но недовольны своим маэстро. Психологическая структура людей, вероятно, не так просто ...

Проблема простой корреляции двух сумм состоит в том, что информация может быть потеряна по ходу, и, в худшем случае, добавив «яблоки к оранжевому». Вы можете фактически опустить связь между переменными.

Использование взвешенных сумм. Вместо этого представляется разумным сопоставить какие-то суммы, чтобы "структура" переменных в двух наборах отражалась весами. Например, если удовлетворенность служанки лишь незначительно связана с удовлетворенностью работой, а удовлетворенность финансовой ситуацией тесно связана с удовлетворенностью работой, тогда я мог бы присвоить меньший вес первому фактору и больший вес другому фактору. Мы можем выразить этот идеал с помощью следующего уравнения:

a1 * y1 + a2 * y2 + ... + ap * yp = b1 * x1 + b2 * x2 + ... + bq * xq

Если у нас есть два набора переменных, первый из которых содержит переменные p , а второй содержит q переменных, мы бы хотели сопоставить сытые суммы с каждой стороны уравнения.

Весовое задание. Мы сформулировали общее «модельное уравнение» для канонической корреляции. Единственная проблема заключается в том, как определить вес для двух наборов переменных. Представляется целесообразным присваивать веса, чтобы две рассматриваемые суммы взвешивания не коррелировали друг с другом. Разумный подход, по-видимому, налагает условие, что две взвешенные суммы должны быть максимально коррелированы. Это именно канонический анализ, основанный на полной корреляционной матрице всех переменных.

Элементы и канонические переменные

В терминологии канонического корреляционного анализа взвешенные суммы определяют корень или каноническую переменную . Можно предположить, что канонические переменные (взвешенные суммы) описывают некоторые «скрытые» переменные. Например, если для набора различных показателей удовлетворенности мы получили весовой мост с большими весами для всех показателей, связанных с работой, мы могли бы сделать вывод, что соответствующая каноническая переменная измеряет удовлетворенность работой.

Количество элементов

До сих пор мы признавали, что существует только один набор весов (взвешенных сумм), который можно вывести из двух рассмотренных наборов переменных. Однако мы можем представить, что для удовлетворения нашей работы у нас есть конкретные вопросы об удовлетворенности зарплатой и вопросы, связанные с удовлетворением социальными отношениями с другими работниками. Возможно, что коэффициенты удовлетворенности коррелируют с удовлетворенностью финансовым положением, а показатели электронного удовлетворения от социальных отношений соотносятся с заявленной удовлетворенностью мужа. Если это так, чтобы передать структуру удовлетворения «zoono», мы должны фактически разделить две взвешенные суммы.

Действительно, расчеты, касающиеся анализа канонической корреляции, приводят к более чем одному набору взвешенных сумм. Короче говоря, количество извлеченных элементов будет равно минимальному количеству переменных, в которых находятся коллекции. Например, если у нас есть три показателя удовлетворенности работой и семь общих показателей удовлетворенности, будут четко определены три канонических корня.

Идентификация элементов

Как упоминалось ранее, программа будет изолировать элементы таким образом, чтобы результирующая корреляция между каноническими переменными была максимальной. Если элемент больше, чем один, то следующий корневой элемент объяснит дополнительную специфичность переменной в двух наборах переменных. Таким образом, последовательно изолированные канонические корни будут некоррелированы друг с другом, и они будут объяснять все меньшую и меньшую изменчивость.

Похожие